The Third Dimension of Random Vibration Control

ABSTRACT

Random vibration testing is the industry workhorse for simulating the environment for a broad range of products. Tests are typically specified by defining a spectrum shape and overall RMS amplitude. The test controller then causes a measured reference acceleration to match these specified parameters. The controller forces a shaped-random response with a normal or Gaussian amplitude distribution. However, experience has shown that such tests may be too conservative for some product/environment combinations; the test does not produce the same damage statistics observed in the field. Adding a third control dimension provides more realistic random vibration tests that better match the damage potential of the actual environment. That third dimension is Kurtosis control, which matches the amplitude distribution of the test to that of the environment.

INTRODUCTION

Random vibration testing as used today is largely unchanged in technique since it was introduced in the early 1950s. It attempts to capture the essence of the service vibration environment for a product and reproduce a similar environment in the test lab. It does this by summarizing the test environment using a frequency spectrum, which gives the relative weighting of each frequency band, and an averaged overall signal intensity. The frequency spectrum is typically defined as an acceleration power spectral density (PSD), and the overall signal intensity is defined as a root-mean-squared (RMS) averaged acceleration. The primary advantage of random vibration testing is that it produces a waveform similar in appearance to those actually measured in the field.

However, despite the similarity of random test and environmental waveforms, it is increasingly being recognized that current random test specifications do not capture the field vibration environment with sufficient intensity for many tests. For example, in the automotive world, technicians often see that random tests do not find product faults that should show up when vibration testing. To make random testing more effective, they sometimes take the random spectrum and increase the intensity level according to their own internal, home-cooked formula. The intensity level may be increased so the random peak g levels match the real world.

Another method to rectify this situation is to use a Field Data Replication (FDR) technique, where the actual waveform measured in the field is reproduced on a shaker in the lab. This method can be extremely useful for many tests. However, critics of this technique claim that since the waveform produced in the test is always the same as one field measurement, it doesn’t capture the variability which can actually occur in the field. For example, each lap around the track will produce a different vibration waveform, so simply recording a single lap and repeating that lap many times on your shaker removes the variability. Also, the large amount of data involved makes it difficult to define a standard and makes it difficult to define the pass/fail criteria for the test. Because of this, there are still very few test specifications based on FDR techniques.

What, in summary, is the problem with current random techniques? Experience suggests very strongly that the problem is the inability to reproduce the peak accelerations which occur in the actual use of a product. The solution to this problem lies in adding a third control parameter to the vibration tests. Presently, current random techniques are controlled by two parameters – one which controls the frequency content of the PSD spectrum and a second which controls the overall test amplitude (the RMS values). By adding a third control parameter – a kurtosis control parameter – one could control the amount of time the random vibration test runs at higher RMS values. This would provide the desired peak accelerations which cause the real-life product failures that are presently being missed by the current random vibration techniques.

INDUSTRY HISTORY

Present-day methods of random testing assume a Gaussian mode of distribution of random data. Modern controllers run random vibration tests with the majority of the RMS values near the mean RMS level, thus vibrating the product only for a short time at peak RMS values. In fact, a Gaussian waveform will instantaneously exceed three times the RMS level only 0.27% of the time. When measuring field data, the situation can be considerably different, with amplitudes exceeding three times the RMS level as much as 1.5% of the time. This difference can be significant since it has also been reported that most fatigue damage is generated by accelerations in the range of two to four times the RMS level (ref. 1). Significantly reducing the amount of time spent near these peak values by using a Gaussian distribution can therefore result in significantly reducing the amount of fatigue damage caused by the test relative to what the product will experience in the real world. Gaussian distribution, therefore, is not very realistic.

This Gaussian distribution has been in use since the infancy of random vibration testing and continues to be used in the present-day industry for several reasons. First, the linear filtering of one Gaussian distribution will result in another Gaussian distribution. So spectrum shaping and the shaker frequency response function do not change the amplitude distribution. This linear transformation property also means that Gaussian data in the time domain transformed through a Fourier Fast Transform (FFT) (as is done in digital random control systems) will result in Gaussian distributions in the frequency domain. Secondly, a Gaussian distribution can be completely determined by two parameters – the mean and standard deviation. In a random vibration context, the mean (the average acceleration) is always zero. Therefore, the Gaussian distribution of a standard random vibration test can be completely defined using a single parameter – the standard deviation (the RMS acceleration). Gaussian distribution is used, therefore, because of its simplicity.

A BETTER METHOD THAN GAUSSIAN DISTRIBUTION – KURTOSIS

To understand a new method that can be used to improve upon Gaussian distribution, it is important to review the meaning and significance of a statistical term – kurtosis.

Kurtosis is a statistical term used to describe the relative distribution of data. Kurtosis is defined as the ratio of statistical moments. Normalized kurtosis is defined as the fourth statistical moment divided by the square of the second statistical moment. This is done to remove variability due to waveform amplitude from the measurement. In this normalized form, the kurtosis for Gaussian data is always 3, regardless of the RMS level or PSD. 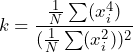The normalized kurtosis value k can be easily computed from N samples of zero-mean waveform data, x_i, using Equation 1.

If your data is not zero-mean, you can subtract off the mean prior to the above calculation. Therefore, true Gaussian data will have a kurtosis value of 3.

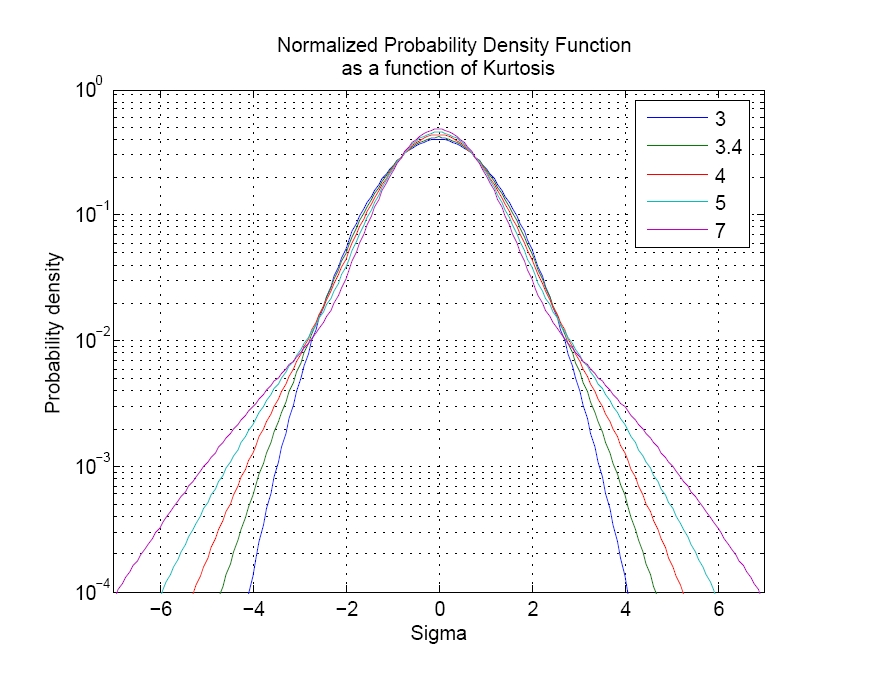
Graphically speaking, kurtosis is a measurement of the size of the distribution’s “tails”. A set of data with a high kurtosis value will produce a distribution curve with higher peak value at the mean and longer “tails”, or in other words, more data points at the extreme values from the mean (Figure 1).

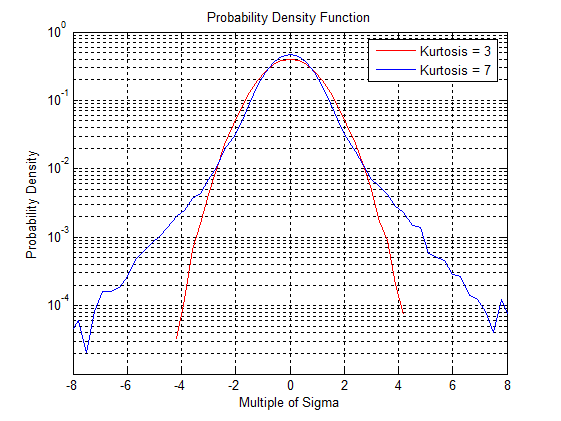
Figure 1. A comparison of kurtosis values 3 and 7. Note how the higher kurtosis value includes higher sigma values (higher peak accelerations).

Gaussian distribution of a standard random vibration test can be shown to inadequately represent real-world data, and since Gaussian distribution can be completely defined using a single parameter (the standard deviation or RMS acceleration), it is useful to consider additional parameters. Ideally, a single additional number could be added to the test specification to capture the probability density distribution for the peaks. What mathematical manipulation could possibly do this? In terms of statistical parameters, the mean is the first statistical moment, and the RMS is the square root of the second statistical moment. So an obvious extension is to consider matching additional statistical moments between the lab distribution and the distribution of the field data. For symmetric distributions centered around zero, the third statistical moment (also called the ‘skewness’) will be zero. The fourth statistical moment (also called the kurtosis) is sensitive to the increased probability of peaks. In fact, this parameter is sometimes also referred to as the “peakiness” factor, and as such, is a desirable parameter to include in the random controller to better match the PDF of the field data. In fact, it may even be a required parameter for a random test to be realistic.

A better method of testing products than using the Gaussian distribution of data is to adjust the distribution of data to more closely fit the real-world data by adjusting the kurtosis level. The difference between the Gaussian distribution and a higher kurtosis value is simply the amount of time spent at or near the peak levels. Adjusting the kurtosis level to match the measured field level will result in a more realistic test.

REAL-WORLD STATISTICS SHOW THE NEED FOR KURTOSIS CONTROL

Demonstrating Real-World Data Is Non-Gaussian

 To demonstrate that field data are often significantly non-Gaussian, data was collected from a series of 40 measurements in four different environments:

• Automotive: 1999 Oldsmobile Bravada (Trial Number 1-13)
• Aeronautical: 2004 Cessna Syklane 182 Turbo (Trial Number 14-24)
• Agricultural: TS110 New Holland Tractor and Celery Harvester (Trial Number 25-37)
• Industrial: Ground Heater-Diesel, single-cylinder generator, Kubota engine (Trial Number 38-40)

Accelerometers were mounted on various locations (windows, dashboards, armrests, steering column, power take-off motor, loader frame, engine bracket, etc.), and the vibration environment was measured using a data recorder software program. The kurtosis values computed for all 40 measurements are shown in Figure 2. Of the 40 different data sets, 58% of the data had a kurtosis level greater than 3.3, for which kurtosis reproduction will have a significant effect.

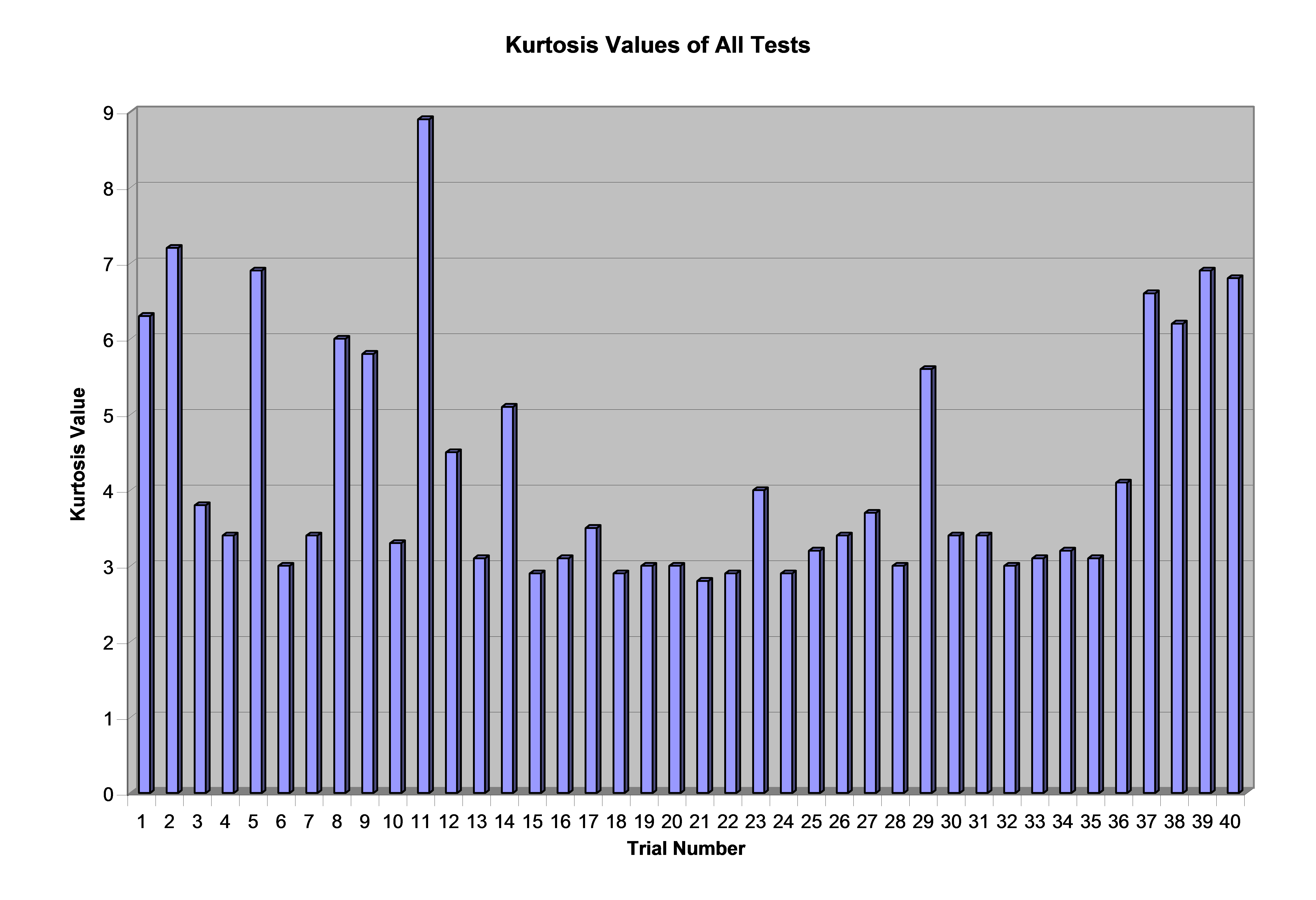
Figure 2. Kurtosis values for 40 tests conducted by Vibration Research Corporation (VRC); note the variety of kurtosis values and that 23 tests have k > 3.3.

The results corroborate previous results of others (ref. 1, 2, 3). While a Gaussian probability density function may be sufficient in some cases, the field data are often significantly non-Gaussian.

Using Kurtosis Control to Match Real-World Distribution

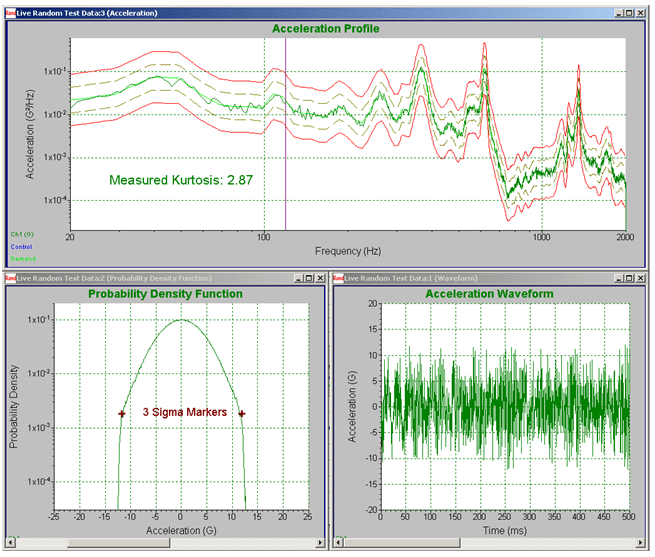
An example of real-world data was examined in terms of its Probability Density Function (PDF) spectrum and compared to a standard controller produced Gaussian distribution and a kurtosis controlled distribution. Data was collected for the acceleration of an automotive dashboard while driving on a gravel road. These measurements were imported into a random vibration control software program, which calculated an average PSD and the kurtosis of the measured data. From these measurements, the kurtosis was evaluated to be 3.8, indicating this environment was non-Gaussian.

Then, using a vibration controller, two random tests were run intending to match this environment. Both tests were controlled to the same measured PSD spectrum and overall RMS values. In one test, a standard algorithm producing a Gaussian signal was used. In the second, a kurtosis control algorithm was used to match the measured 3.8 value.

As shown in Figure 3, the PDF of the kurtosis-controlled test produced a far better match to the field measurements than the Gaussian-controlled test. Note that the field measurement and kurtosis-controlled test both exhibit broader PDF “tails” than the Gaussian test. These tails indicate the measured environment was more severe than the Gaussian test intended to represent it.

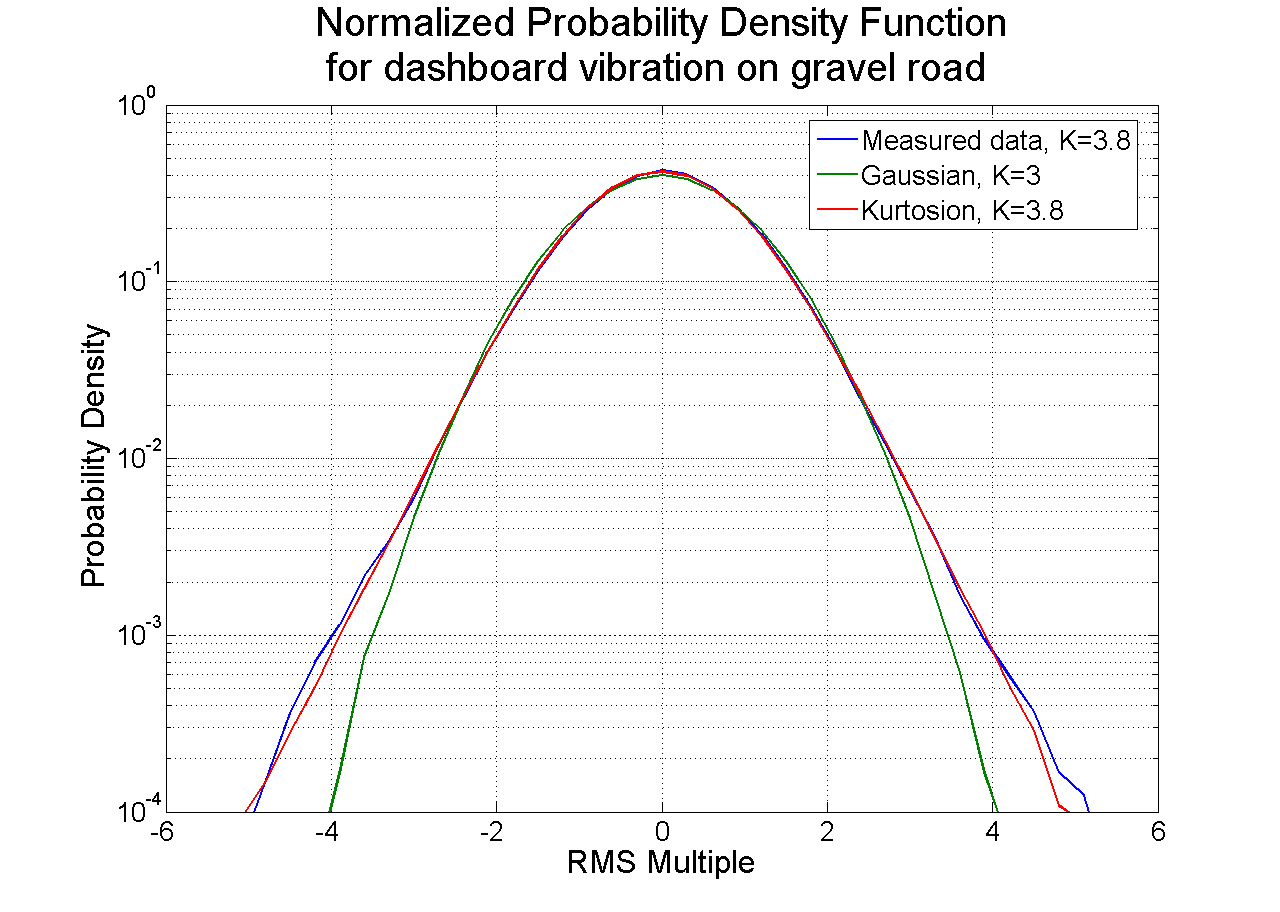
Figure 3. Probability density function for measured field data compared with that produced by random vibration testing with and without matching kurtosis. When the kurtosis is matched, the probability density function reproduced in the lab environment matches much more closely to field measurements.

DEVELOPMENT OF THE THIRD DIMENSION OF RANDOM VIBRATION CONTROL

The latest modification in random vibration testing is patented Kurtosion®, a closed-loop method of kurtosis control developed by Vibration Research. This method will permit the adjustment of the kurtosis levels while maintaining the same testing profile and spectrum attributes. With this new technique, in addition to the standard random test PDF and RMS parameters, a kurtosis parameter is now defined to produce a test in the lab. This is similar to current random tests but is one step closer to the vibrations measured in the field. This kurtosis parameter can be easily measured from field data using Equation 1 in the same manner as the RMS and PDF are currently determined from field data.

This technique begins with a statistical distribution that is similar in shape to the distributions seen in field-measured data and which has a variable kurtosis level controlled by a single parameter. The distribution used is plotted in Figure 4 for a sampling of kurtosis values. As can be seen in Figure 4, the ‘tails’ of the distribution are extended to achieve the increased kurtosis the same way as the ‘tails’ are extended in non-Gaussian field measurements.

Figure 4. The normalized probability density function for a set of data, plotted for several kurtosis values.

The kurtosis parameter shifts the distribution smoothly over the full range from Gaussian through high kurtosis levels. A feedback control loop can be implemented in the controller to achieve the desired kurtosis level in the acceleration waveform. It is important to implement feedback control on the acceleration measurements because the kurtosis level at the controller output will typically be different from that in the acceleration waveform. Without the feedback control, you could set the kurtosis of the controller output signal, but this would not achieve the desired kurtosis on your shaker.

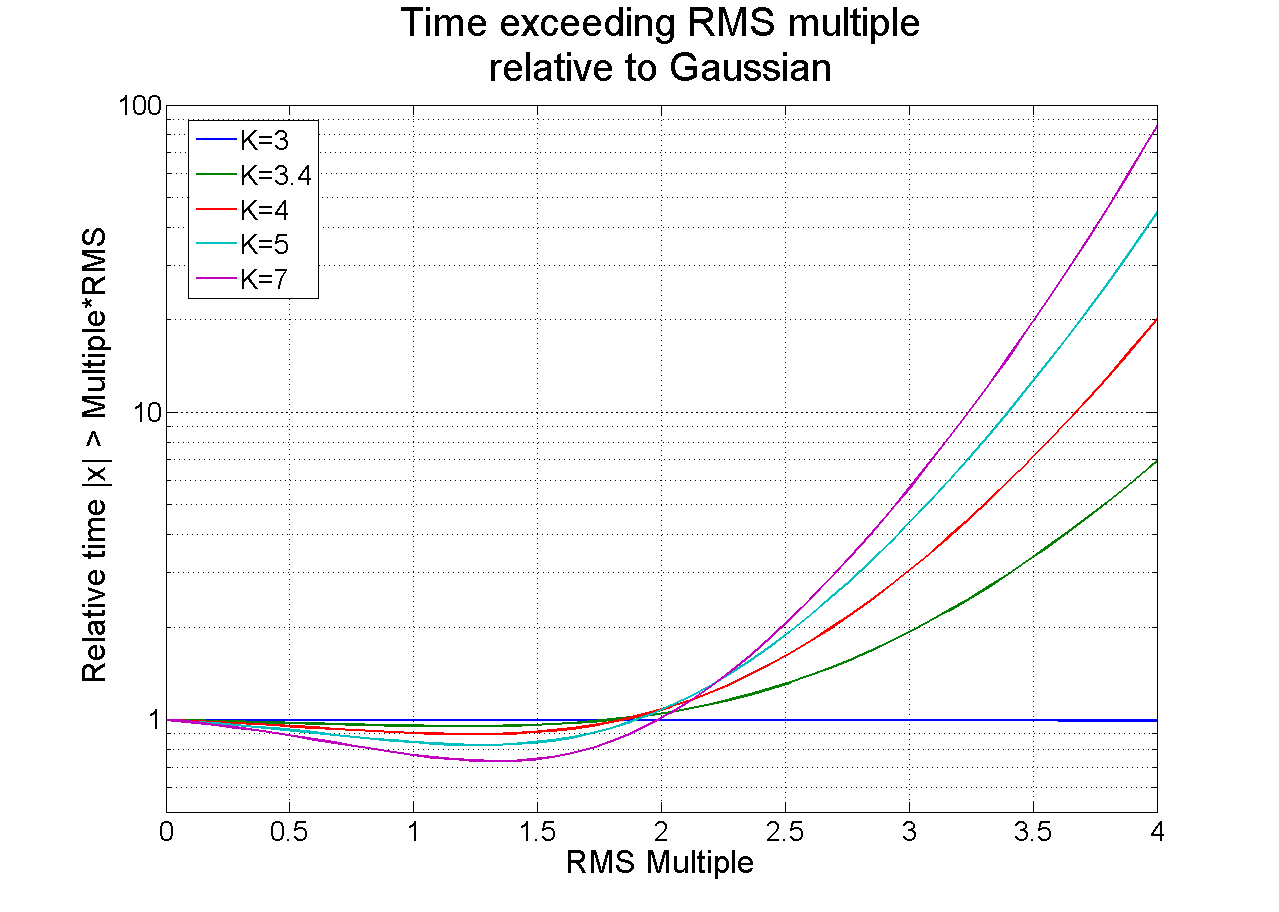
An alternative view of the distribution is plotted in Figure 5, where the probability of exceeding an absolute-value amplitude is shown. This view is interesting because it is readily evident that the kurtosis parameter directly translates to an increase in the time spent at higher amplitudes. Note that the traces cross at twice the RMS value, with a probability of 4.6%. For the chosen family of distributions, regardless of the kurtosis, the instantaneous acceleration is less than twice the RMS value for 95.4% of the test time. The most damaging events occur at higher levels that represent less than 5% of the test duration. Kurtosis strongly affects the severity of these events.

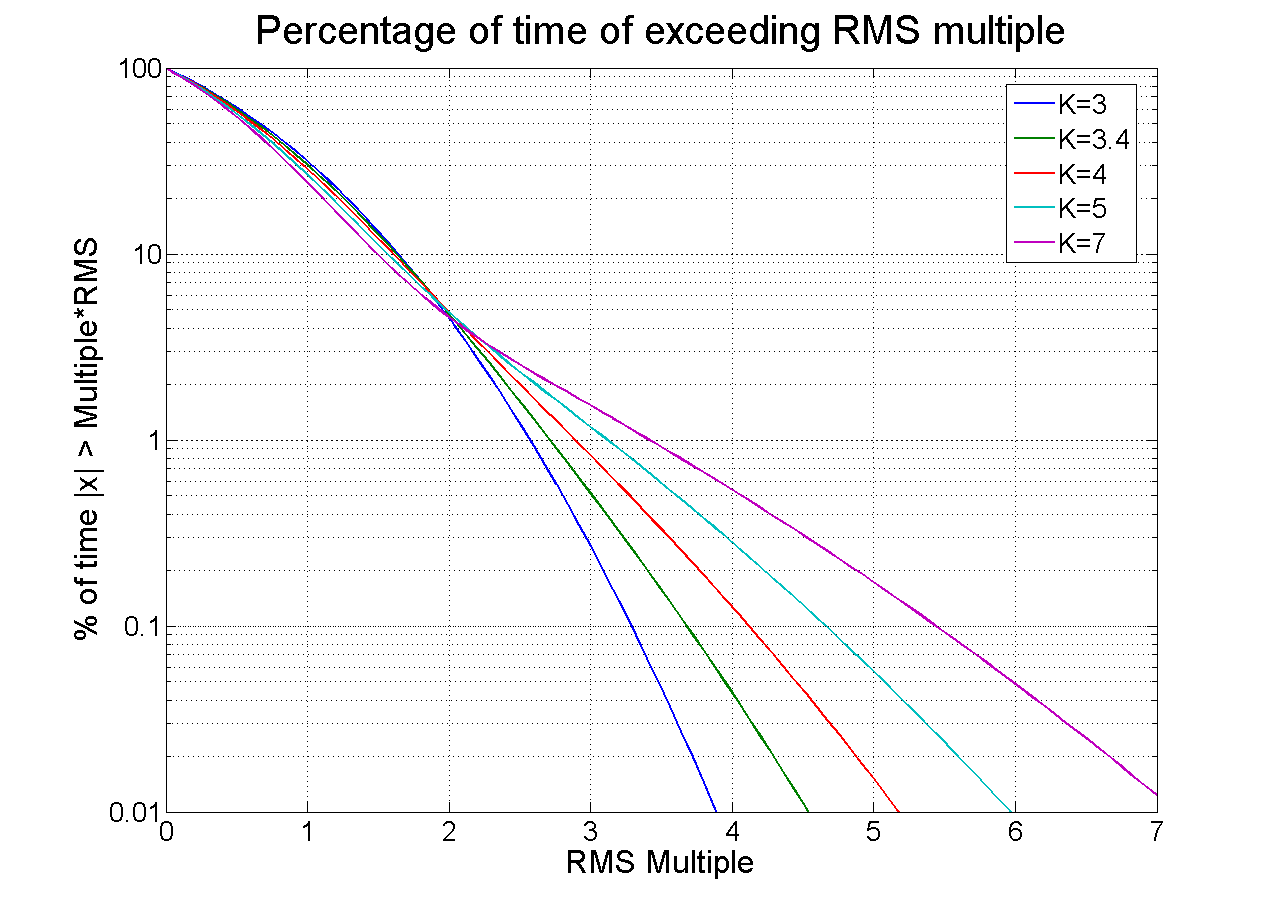
Figure 5. Percentage of time spent above multiples of the RMS level, plotted for several values of kurtosis. Higher kurtosis levels significantly increase the amount of time spent at or near peak levels.

For example, a Gaussian distribution (kurtosis = 3) spends only 0.27% of the time above three times the RMS level. Increasing the kurtosis to four will increase this time to 0.83% while increasing the kurtosis to seven increases this time to 1.5%. This may not sound like much, but consider that during a 1-hour test, the test article will be approaching a full minute at levels above three sigma, rather than below three sigma. This statistic can translate to significant product stresses. These stresses will not occur with a traditional Gaussian distribution but do occur in a real environment.

To illustrate this point, we divide each vertical amplitude in Figure 5 by the amplitude for k = 3 (the Gaussian case) to get the relative time above absolute value versus three sigma for each value of k. This is plotted in Figure 6, where we can clearly see that with increased kurtosis, the relative amount of time spent at the higher levels is increased many times over the Gaussian case.

Figure 6. Illustrating how kurtosis increases time spent at higher levels.

A second aspect of the technique is that the PSD and RMS levels can be controlled in a manner similar to standard random tests. Any tests previously run with standard random controller systems can now also be run with the same PSD specifications with a user-defined kurtosis value. Not only does the new technique maintain the same frequency spectrum, but it also operates so that the kurtosis of the acceleration waveform can be adjusted without affecting or distorting the frequency spectrum. As a result, the kurtosis feedback control loop can operate independently from the standard random spectrum control without any effect on the spectrum.

This can be illustrated by considering the controller software screenshots of the frequency spectrum (the acceleration spectrum profile) for a celery harvester (Figures 7 and 8). In Figure 7, a standard Gaussian distribution with 3 sigma clipping is shown. In Figure 8, the same field-recorded data is shown with kurtosis control set at a kurtosis level of 5. Notice that the acceleration profile spectrum is identical in both cases, even though the kurtosis levels are different. This demonstrates the important second aspect of the kurtosis control technique – the PSD and RMS levels are not affected by an adjustment in kurtosis levels.

Figure 7. Harvester acceleration profile with Gaussian Distribution and 3 sigma clipping.

Figure 8. Harvester acceleration profile with kurtosis = 5.

A third aspect of the technique is that the kurtosis is introduced in a manner that ensures that all frequencies in the test spectrum have an increased kurtosis. This is an important property because most objects under test have narrow-band resonances. The kurtosis must be increased at the resonance frequencies or the resonances will not see the resulting increased peak amplitudes, and the results at that frequency will be no different from standard random control techniques. This new technique increases the kurtosis across the entire bandwidth of the random test, including the resonant frequencies of the object under test.

A fourth aspect of the technique is that the controller dynamic range is unchanged by the kurtosis control. The new method does not contain any nonlinear elements and therefore does not introduce harmonic distortion into the test. Since harmonic distortion is the primary factor limiting dynamic range in random vibration controllers, it is important that it be avoided in the control algorithm. For example, harmonic distortion of only 0.003% will limit the achievable dynamic range of a random vibration control system to 90 dB. Since the new technique doesn’t add any harmonic distortion, the dynamic range of the resulting control system remains limited only by the harmonic distortion of the accompanying analog electronics. The new technique has the same dynamic range characteristics as a standard random vibration controller system.

To demonstrate the third and fourth aspects of this new kurtosis technique, a random vibration test was run with standard Gaussian random control (kurtosis = 3) and then also with kurtosis = 5, with kurtosis applied to frequencies above 10 Hz. The breakpoints for this profile are listed in Table 1. For sake of comparison, the proposed non-linear method of kurtosis control (ref. 3) was also computed for skewness = 0 and kurtosis = 5.

Table 1. Breakpoints for Dynamic Range Test

To examine the relationship between kurtosis and frequency, the data were separated into one-third octave bands, and the kurtosis of each band was computed. These results are plotted in Figure 9. This definitively demonstrates that the new kurtosis control method increases the kurtosis across the entire frequency band for the test, while the other non-linear kurtosis method actually shows no increase over any single narrow band. This demonstrates the important third aspect of the new method of kurtosis control – that kurtosis increases across the entire bandwidth of the random test, including the resonant frequencies of the object under test.

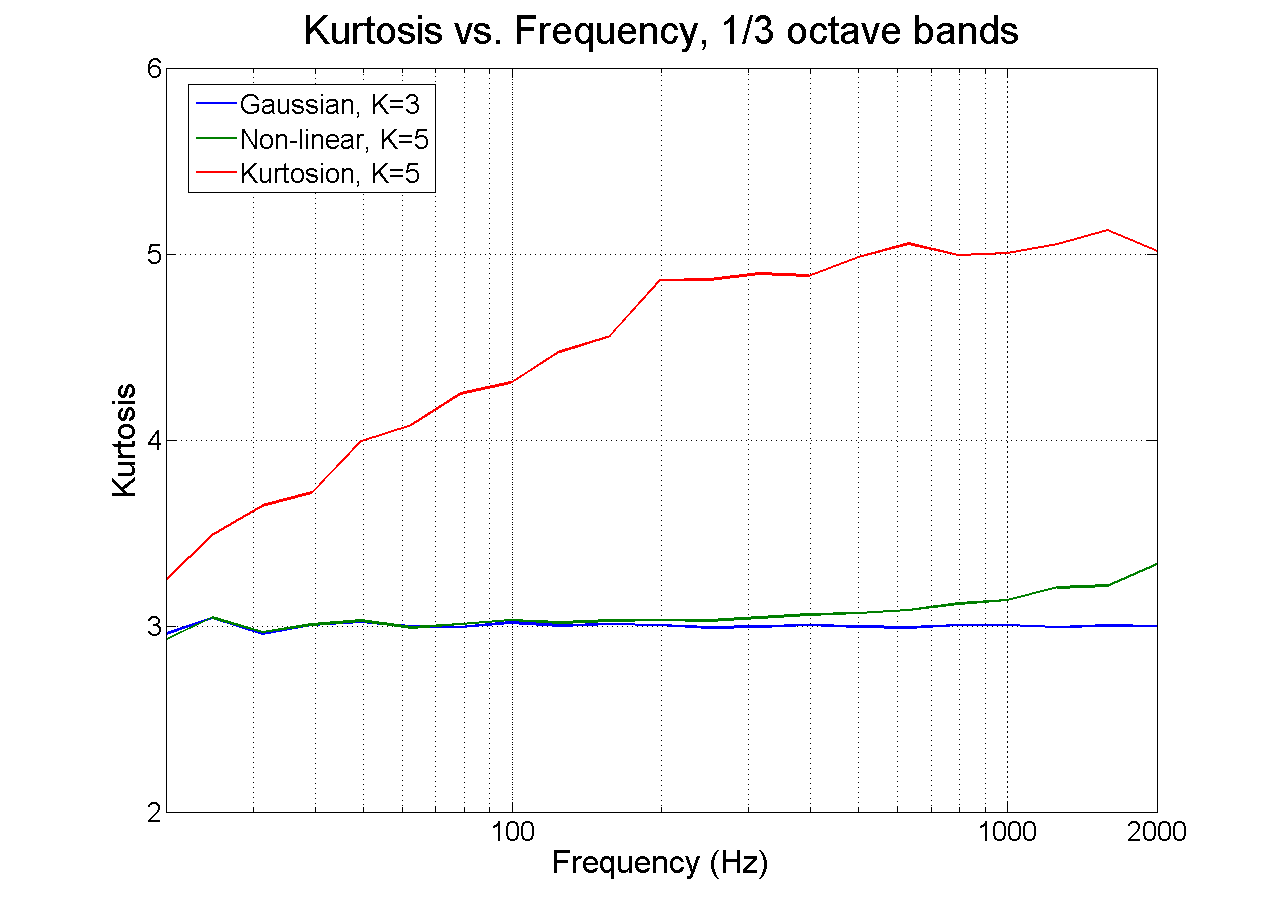
Figure 9. Kurtosis measured in one-third-octave bands for the standard Gaussian random control (kurtosis = 3), for the new method with kurtosis = 5, and for the previous nonlinear method. The new method increases kurtosis through the frequency band of the test.

Figure 10 demonstrates the benefits of the fourth aspect of the new kurtosis control technique. It shows that the spectrum with the new technique is unchanged by the increase in kurtosis, demonstrating that the same PSD with the same dynamic range is achieved regardless of kurtosis level. In fact, the spectrum control is unchanged by the kurtosis change, so it is possible to change the kurtosis from 3 to 5 to 7 (and beyond) without any change in the resulting spectrum. In contrast, the proposed non-linear technique shows a significant loss in dynamic range, so that only 23 dB of the dynamic range remains.

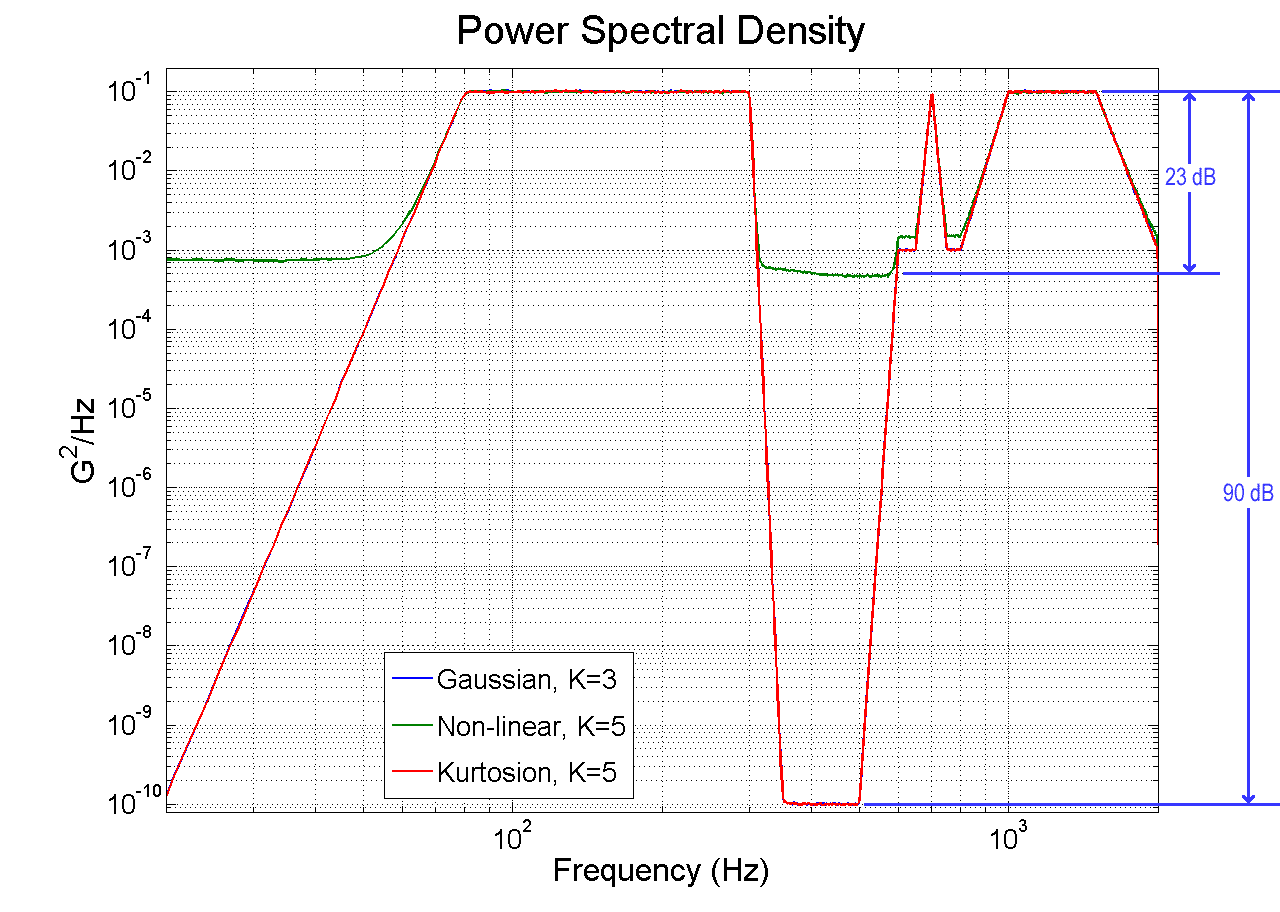
Figure 10. Power spectral density plot for a new method, plotted for kurtosis value of 5, compared to both standard Gaussian random control (kurtosis = 3) and for the previous non-linear method. The new method maintains the controller dynamic range while the non-linear method severely limits dynamic range.

EXPERIMENTAL RESULTS

 The obvious question is “what significance does this have to vibration testing?” The bottom line in vibration testing is that the testing should highlight potential field failure problems early in development before they become issues in the field. If including a kurtosis control parameter does not make a difference in isolating product weaknesses, then it would be a meaningless function. With this in mind, we constructed a simple controlled experiment to investigate the effects of increased kurtosis on time to failure. Ordinary 75-watt light bulbs were chosen as the test item because the failure of a light bulb is readily evident. Light bulbs also are inexpensive, allowing for many test runs to improve the statistical significance of the results.

The PSD used was based on a standard automotive specification, referred to as “body and IP profile,” – a vibration profile for automobile instrument panels – with a modification of extending the bandwidth of the low-frequency energy level out to 100 Hz to encompass the observed 90 Hz resonance frequency present in the light bulbs. The breakpoints for this profile are listed in Table 2. A fixture with two light bulb sockets was mounted to the table of an electrodynamic shaker, as shown in Figure 11.

Table 2. PSD breakpoints used for light bulb test.

Figure 11. Setup for vibration testing of light bulbs with kurtosis.

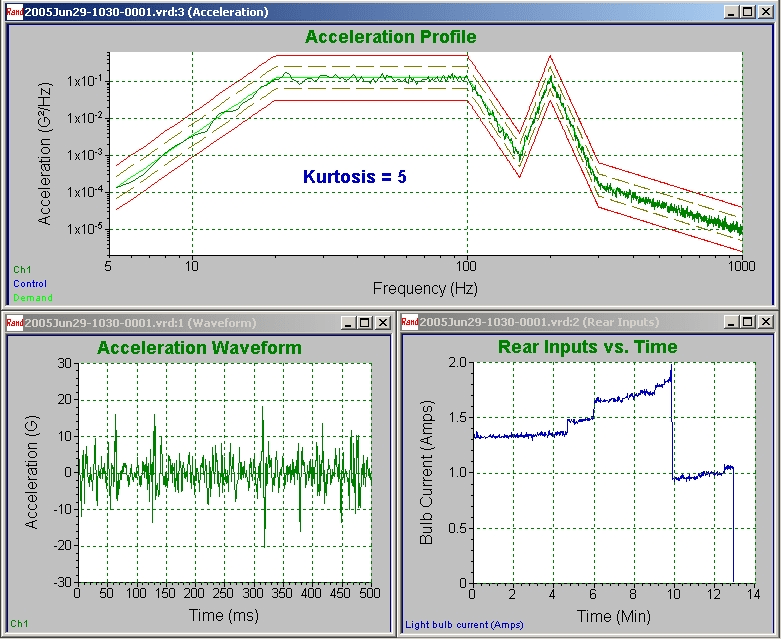
Tests were performed on a total of 66 light bulbs, testing 22 bulbs each at kurtosis levels of 3, 5, and 7. While the vibration test was running, the current through the light bulbs was monitored and plotted on the display. As a light bulb began to fail, the current would increase somewhat. When complete filament failure occurred, the current would drop suddenly. The time to failure was measured as the time from the beginning of the test to the time of the sudden drop in current. Since two bulbs were tested simultaneously, the test was allowed to continue until both bulbs had failed, and then the time to failure was computed individually for each bulb. Sample screenshots from the controller software are shown in Figure 12. Note that the PSD was the same in all cases, while the higher kurtosis levels translated into higher acceleration peak levels and shorter time to failure. Thus, the simple light bulb test clearly demonstrates that a kurtosis control parameter is a significant addition to random vibration testing because while it maintained the same test specifications, it brought the light bulbs to failure sooner.

(a)

(b)

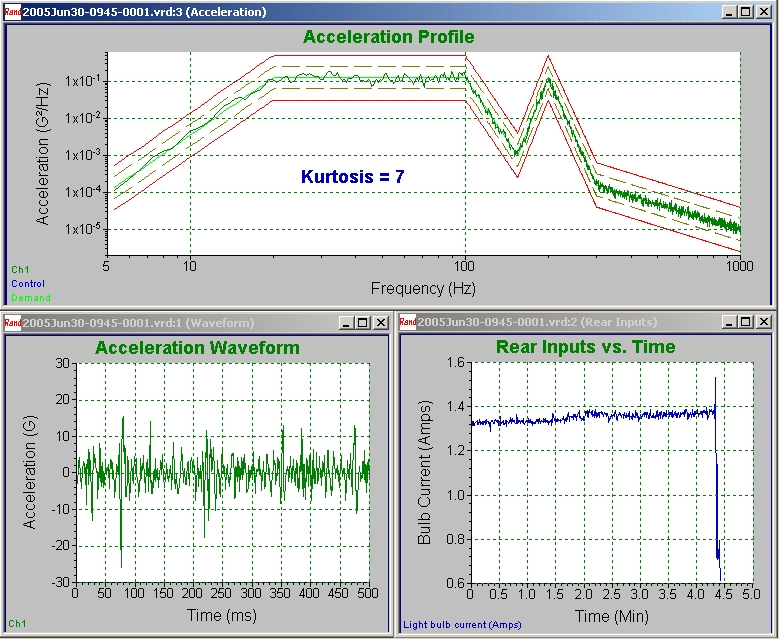
(c) Figure 12. Controller software screenshots of testing at a.) kurtosis = 3; b.) kurtosis = 5; and c.) kurtosis = 7. Note that higher kurtosis levels give the same PSD but result in higher acceleration peak levels and shorter time to failure.

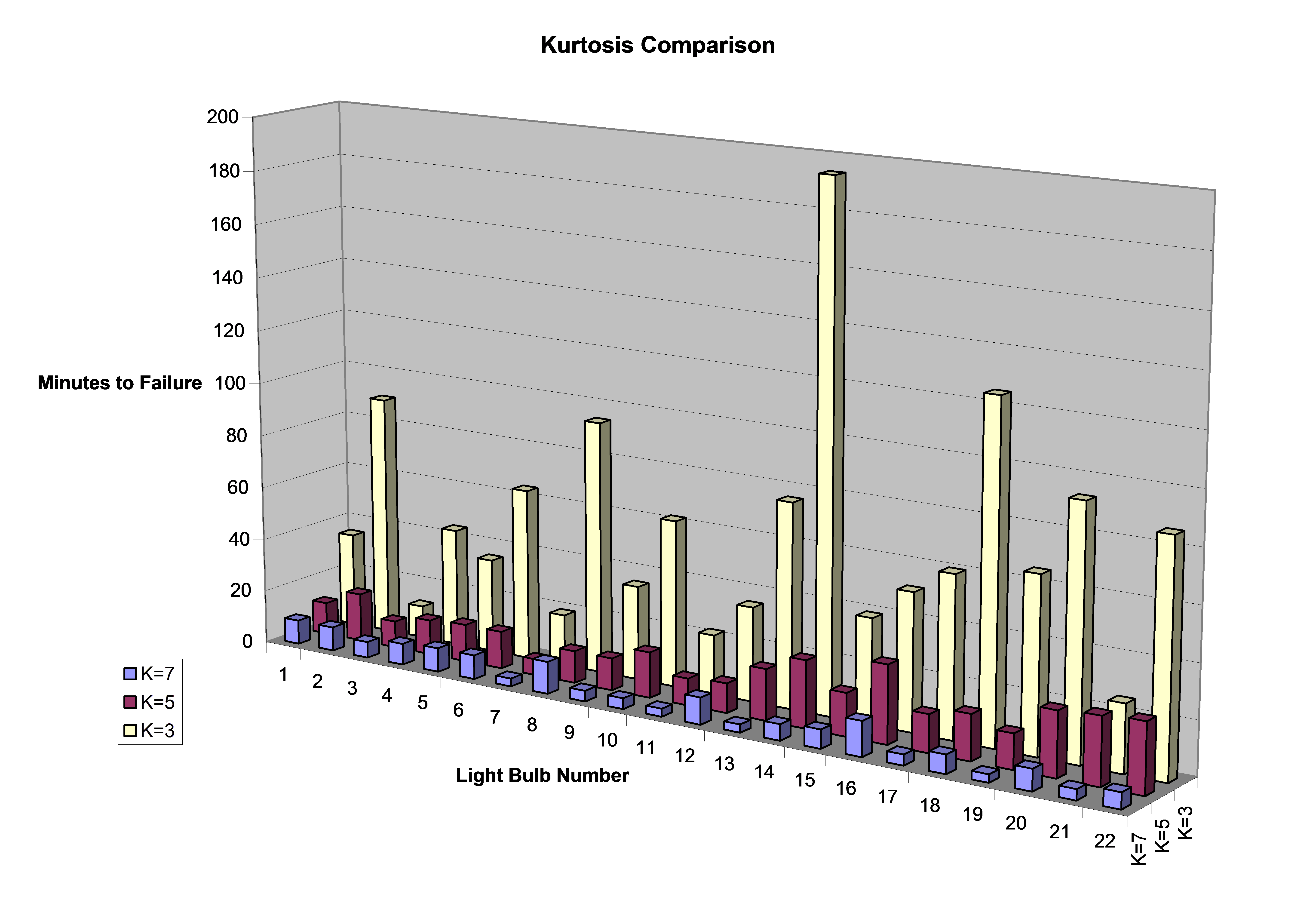
The time to failure for all tests is shown in Figure 13.

Figure 13. Time to failure of all light bulb tests.

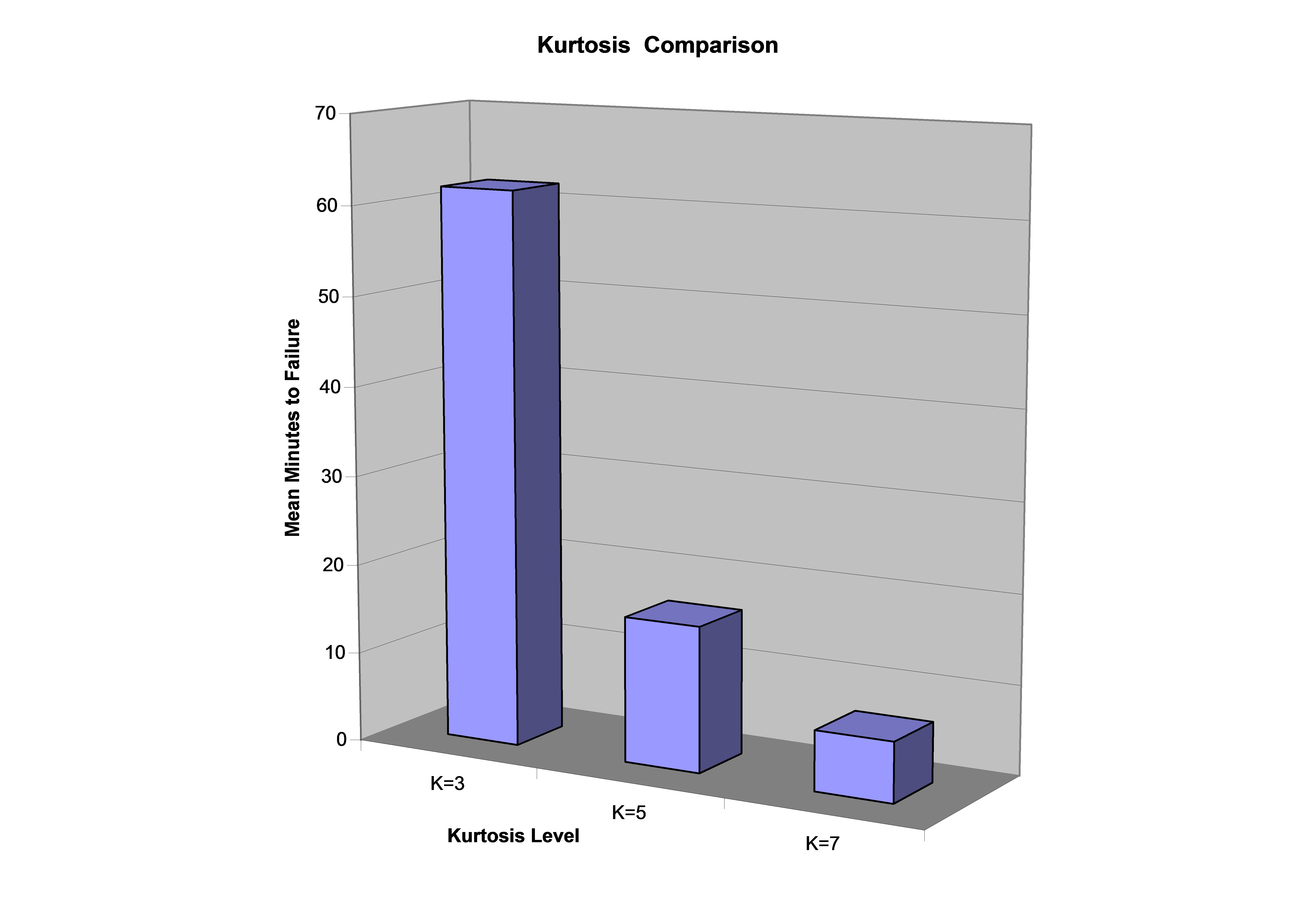
This figure further shows that the time to failure decreased as kurtosis level increased. Taking the average time to failure of the 22 tests at each kurtosis level, it becomes readily evident that the light bulbs are brought to failure significantly faster when the kurtosis is increased, from 62 minutes with kurtosis = 3, to 16 minutes with kurtosis = 5, to 6.7 minutes with kurtosis = 7 (Figure 14).

Figure 14. Mean minutes to light bulb failure.

The light bulb test performed here is a very simple example, but it clearly illustrates the point. Decreased time to failure means that failure modes are more readily produced in lab testing with higher kurtosis levels. It also means that you are more likely to detect potential field failures if you include the kurtosis parameter when performing vibration testing. Now that kurtosis can be easily included in random vibration tests, manufacturers can perform similar case studies on their components to determine how kurtosis can help them in designing more reliable parts.

CONCLUSION

Kurtosis is an exciting new development for random vibration control. Technicians have wanted this realism factor for a long time, even if they did not know what kurtosis was. Before today, there has not been a way to add this important peakiness factor to your random test. Vibration Research Corporation has demonstrated a method for reproducing not only the PSD and RMS levels but also the kurtosis of the field data. We have developed, commercialized, and applied for a patent on this technique. It is very easy to use. The kurtosis is easily measured from field data, and this measurement is the only additional information required for the method to be implemented. The method preserves all the important characteristics needed for random testing, such as PSD, RMS measurement, dynamic range, and uniform distribution of kurtosis over the spectrum. Testing and design engineers are now free to include the desired kurtosis in their random vibration test specifications to increase the realism of their tests, improve the likelihood of detecting failure mechanisms during testing, and therefore, increase the reliability of their designs. Random vibration testing has never been better.

SYMBOLS

PSD – Power Spectral Density

RMS – Root-Mean-Squared

FDR – Field Data Replication

FFT – Fourier Fast Transform

PDF – Probability Density Function

Kurtosion® – Vibration Research’s Trademark name for patented Kurtosis Control Technique.

Authors: John Van Baren, President & Philip Van Baren, VP/Engineering, Vibration Research

Download PDF