Harmonics and Musical Overtones
Instruments produce musical tones through a variety of means. For woodwinds, air is blown into a vibrating column that comprises the body of the instrument. Instrumentalists can adjust the column’s length to adjust the fundamental frequency of the vibration.
Guitars, pianos, and string instruments are similar in that they have strings pulled taut between two fixed locations. The string is excited and oscillates in a stable pattern at its fundamental frequency.
The fundamental frequency (f0) of a string fixed at both ends is a combination of its tension (T), mass (m), and length (L).
(1) 
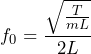
Instrumentalists can adjust these values to change the fundamental of a string before or during excitation. Violinists learn to position their fingers to change the length of the excited string and vary the pitches by half-tones (1/12 octave spacing). To play a note one octave higher than an open string, they position their finger halfway between the nut and the bridge, which make up the first and last nodes for all the standing waves.
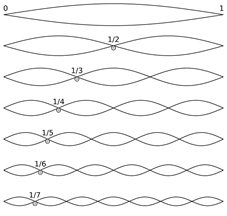
Harmonic partials on a string fixed at both ends. Photo credit: Wikipedia.
Musical notes may sound like one pitch, but they are a mixture of the fundamental and its overtones. A fundamental frequency excites the string’s fundamental harmonic frequency, causing the entire string to oscillate back and forth. Additional frequencies excite other standing wave patterns to produce overtones. These overtones have a wavelength (λn) that is proportional to the string’s length.
(2) 
Overtones produce pitches that follow the harmonic series. For instance, a 440Hz tone (A4) will have overtones at 880Hz (A5), 1320Hz (a slightly sharp E6), 1760Hz (A6), 2200Hz (a slightly flat C#7), 2640Hz (a slightly sharp E7), and so on.
Musically inclined individuals may notice that the first several pitches in a harmonic series will produce a major triad. In the above series, the notes A, C#, and E form an A major triad. When an instrument or a group plays a triad or a consonant chord, other strings or instruments reinforce the overtones of the chord’s root by playing those tones as their fundamentals, generating rich harmony.
Analyzing Overtones in ObserVIEW
ObserVIEW includes octave band graphs. These graphs can filter signals into different frequency ranges and show the comparative strengths of each. These bands can be set to 1/12 octave spacing, making an octave band graph ideal for analyzing overtones for a musical note.
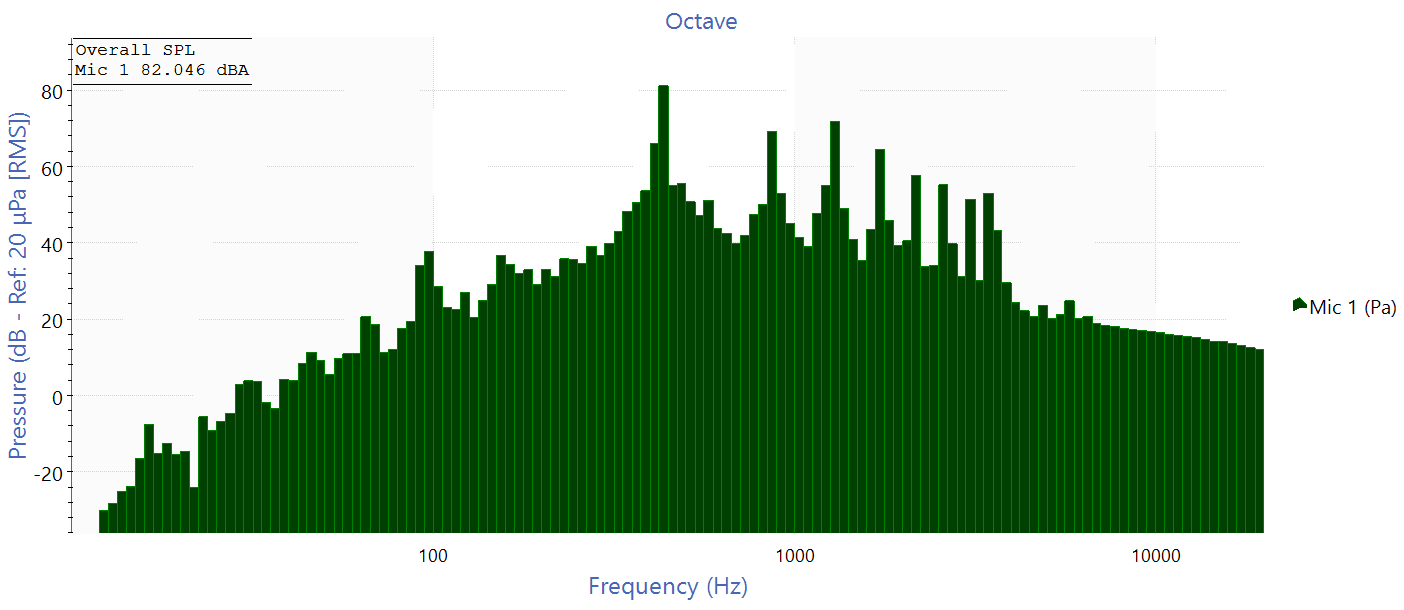
Below is an octave band graph for a single piano note.
Octave band graph for a single piano note.
To match the frequency response of a human ear, an A-weighting curve was applied to the time signal before it was filtered into frequency bins. The Overall SPL annotation shows that the note’s combined perceived loudness at the microphone’s location was just over 82 decibels (dBA).
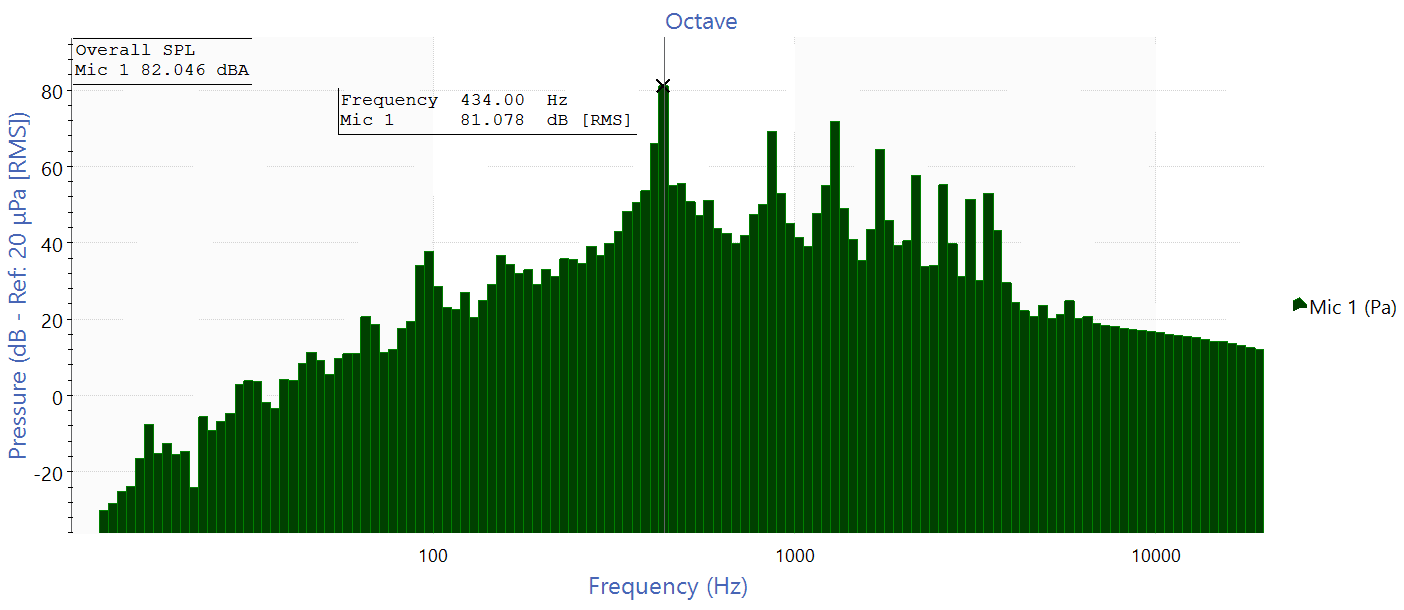
We can view the strength of the fundamental frequency range using a standard cursor.
Octave band graph with a standard cursor.
The strength appears to be just above 81 dBA. This value is reasonable because decibels are logarithmically scaled.
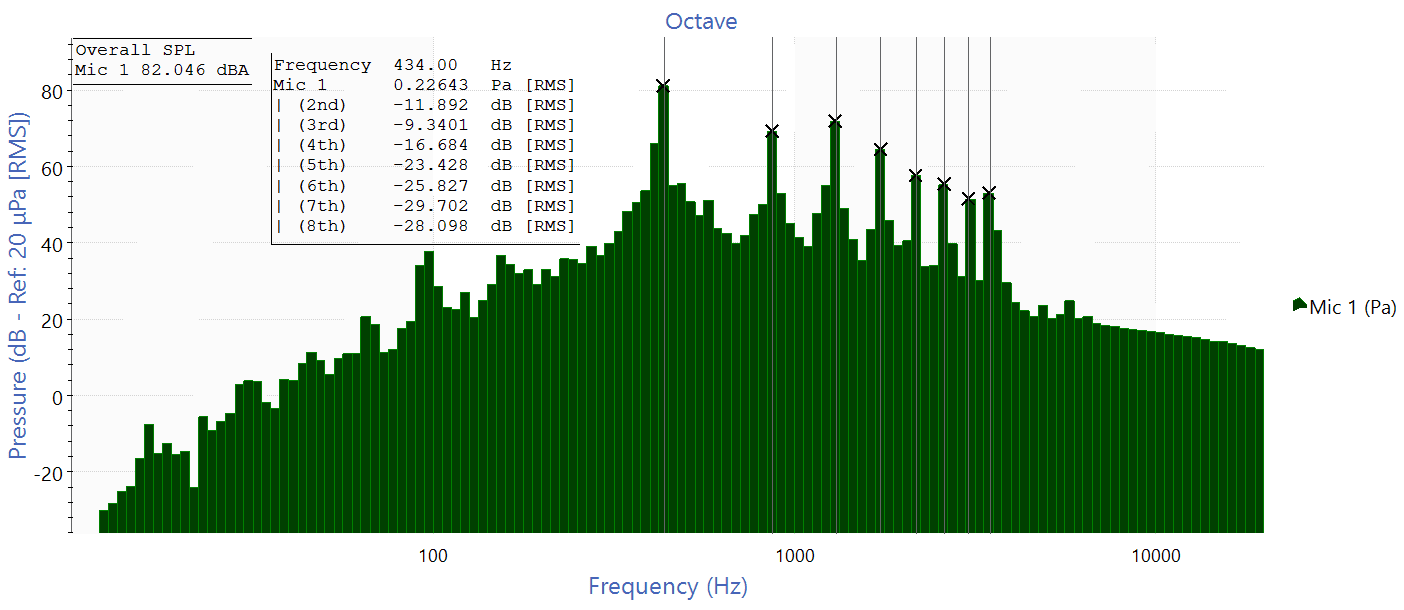
Next, we can use a harmonic cursor to compare each of the harmonics to the fundamental frequency.
Octave band graph with a harmonic cursor.
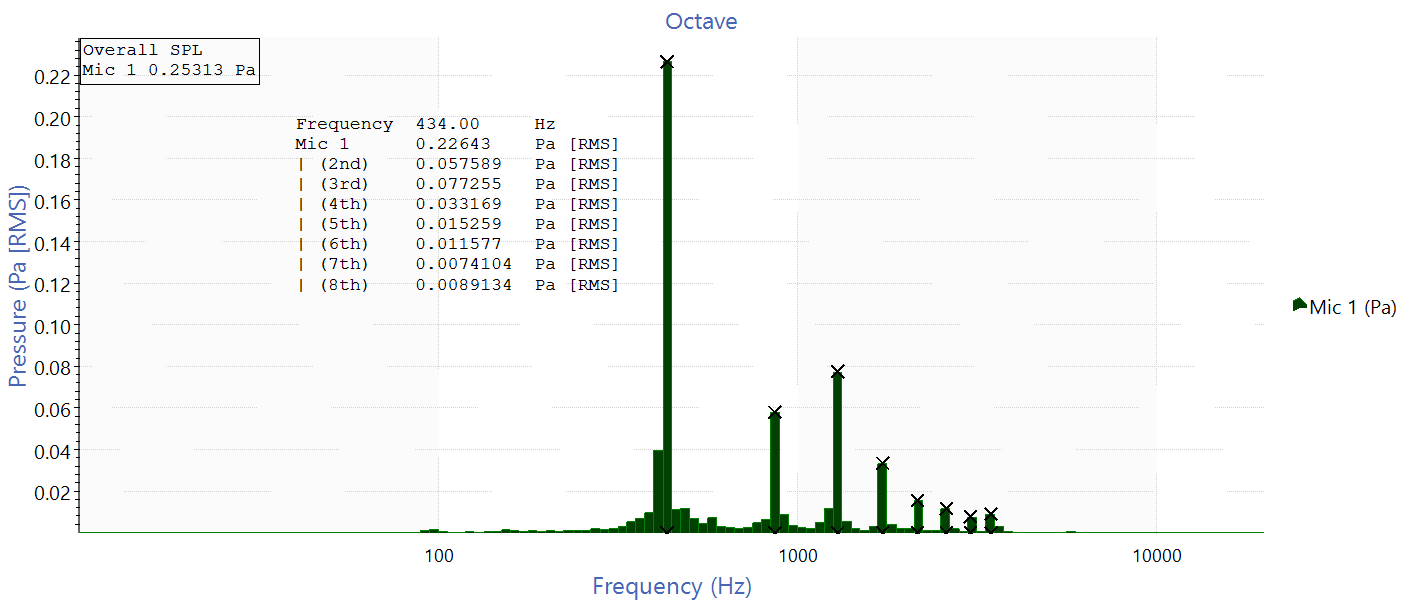
As the annotation shows, each of the overtones has a smaller magnitude than the harmonic. The differences between harmonics appear small; however, a linear scale reveals that the fundamental’s magnitude is over twice that of any overtone.
Octave band graph on a linear scale.
Still, the presence of overtones can greatly modify the perceived sound. The ratio of overtones relates to the difference of perceived sounds of a pure sine tone and a note on a piano or any other instrument.
Below is a comparison between the overtone/fundamental ratios of a piano, oboe, violin, and a computer-generated sine waveform.
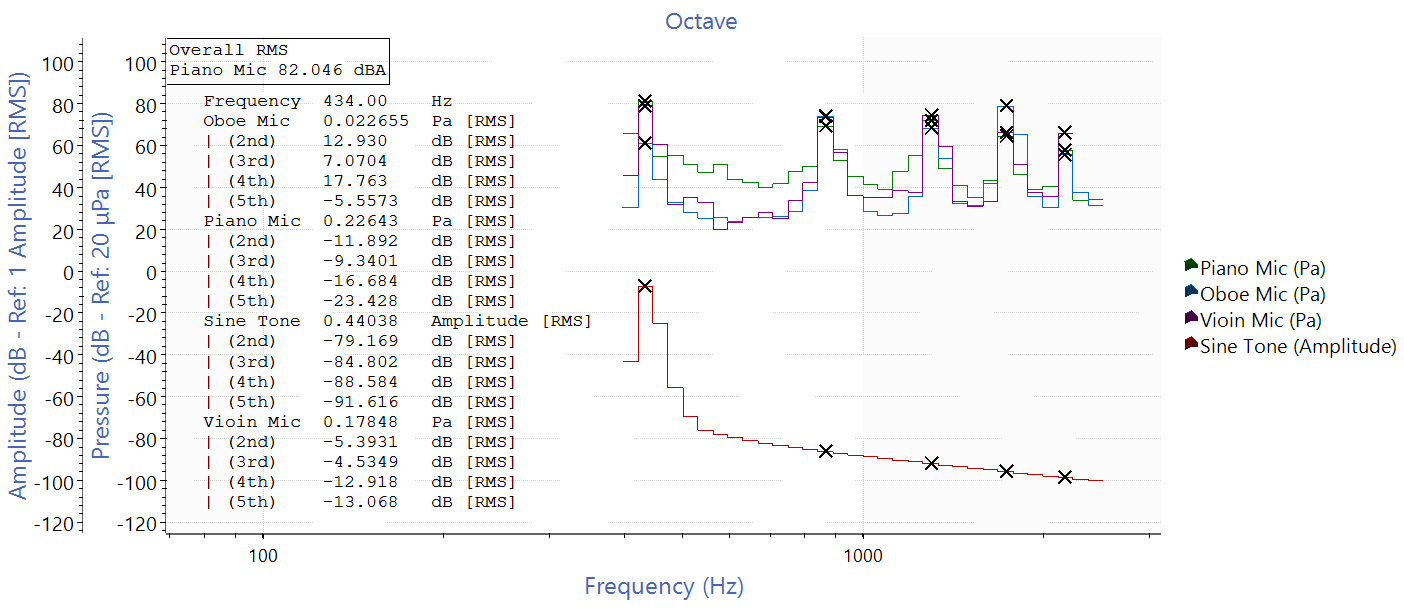
Comparison of the overtone/fundamental ratios of a piano, oboe, violin, and computer-generated sine waveform.
The harmonic cursor displays the relative strength between the base frequency and the overtones. As expected, the sine tone has almost no data in the overtone frequency bins. The oboe, which has a penetrating sound, has overtones where the relative amplitude exceeds the first harmonic. (Since the oboe cannot be approximated as a fixed string instrument, its mechanics and formulas for fundamental frequencies and wavelengths may differ slightly from the other instruments tested, but the general concepts hold true: A medium with resonances based in the harmonic series is being excited to produce sound.) The piano has overtones that are much more subtle in comparison. The violin falls between the two instruments on this scale.