The VibrationVIEW software supports eight synthetic waveforms or a user-defined waveform. A shock response spectrum (SRS) waveform defined by field recorded data will have a similar frequency response function as the original field environment. However, the data is typically derived from multiple data sets, which may not be available/realistic depending on the stage of development, application of the product, or time constraints.
Read: Using Recorded Data to Improve SRS Test Development
In addition to the user-defined waveform, various synthetic waveforms can be used to achieve a required SRS curve. The selection of the pulse type depends on the application. If the test standard does not define the pulse type, the characteristics of the waveforms can be used to help guide your decision.
Below, we define the eight synthetic waveforms supported by our software, including the characteristics of the waveforms and areas of potential utilization. It is important to note that synthetic waveforms are experimental data. Shock tests are often highly specific, so it is difficult to provide standard suggestions for the use of the waveforms. If you still have questions, please feel free to contact us.
Waveforms
Chirp Waveforms
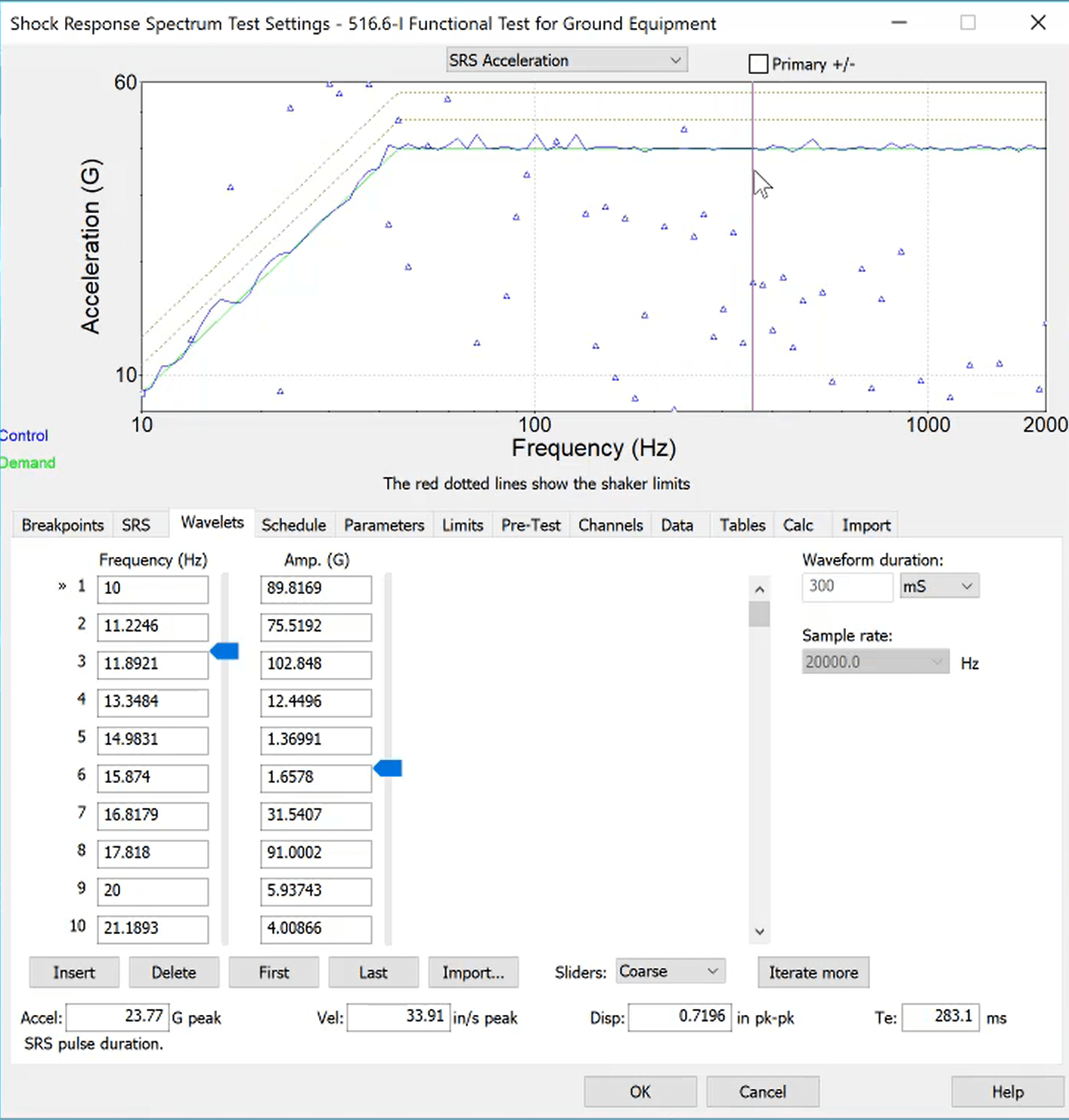 Chirp waveforms change in frequency over time. These signals are deterministic, meaning they can be described—or determined—by a mathematical function. Among other operations, they can be used for frequency identification, modal validation, and high-cycle fatigue testing for resonances.
Chirp waveforms change in frequency over time. These signals are deterministic, meaning they can be described—or determined—by a mathematical function. Among other operations, they can be used for frequency identification, modal validation, and high-cycle fatigue testing for resonances.
Linear Chirp
The linear chirp waveform functions as a frequency sweep. The frequency of the signal varies over time and at a fixed Hz/second rate. The frequency can be swept up (lower to higher) or down (higher to lower).
A linear frequency sweep can be used to identify the natural frequency response of a device under test (DUT) and system resonances. As a time-frequency analysis, this method is useful in the identification of frequency content in linear time-variant systems (Xu).
Linear chirp signals are most useful for testing across small frequency ranges. A shorter timeframe will result in a higher frequency resolution. The linear sweep is a simple method and, therefore, common.
Exponential Chirp
Like the linear chirp, the exponential chirp functions as frequency sweep. The frequency of the signal varies exponentially as a function of time and at a fixed octaves/second rate.
An exponential sweep is most suitable over a wide frequency range where the start and end frequencies are a multiple of 10 or greater apart. The signal covers a wider range over a shorter timeframe and can shorten the pulse length.
Often, deterministic signals are used on linear systems or as a linearity check. Random signals, then, are used in the presence of nonlinearities.
Burst Waveforms
Burst waveforms are random signals defined by their statistical characteristics.
Burst Random
A random signal excites a system using varying amplitude and phase. With a burst random waveform, the random signal is only employed for a portion of the data acquisition.
Burst random waveforms are Gaussian. When employed, they ramp up smoothly, remain at a constant level, and then end with a smooth ramp back to zero. This type of waveform is well suited for long duration earthquake simulations (20 to 30 seconds).
Random signals tend to average slight nonlinearities in a system. While this is beneficial, the signal will not meet the interval requirements of the Fast Fourier Transform (FFT). This can lead to leakage and will require additional windowing operations. With the burst random waveform, however, the signal can be contained within one sample interval and therefore satisfies the FFT requirements (Avitabile).
Enveloped Burst Random
The enveloped burst random waveform is also Gaussian. The signal is enveloped using a ramp up and then exponential decay in amplitude levels. This process generates a waveform that more closely resembles a true earthquake event.
For earthquake simulation tests, the burst random and enveloped burst random methods produce appropriate long duration stationary random waveforms.
Superposition of Chirp Waveforms on the Burst Random Waveform
Linear Chirp on Burst Random and Exponential Chirp on Burst Random
The chirp on burst random waveform is the superposition of either the linear or exponential chirp waveform on the burst random waveform.
With the burst chirp waveform, the chirp signal is turned off before the end of the sampling window. The chirp signal offers greater control over the input amplitude and frequency, while the burst excitation provides a shorter test time and the reduced possibility of leakage. In “Vibrations and Acoustics: Measurement and Signal Analysis,” C. Sujatha writes, “This excitation technique offers a very good compromise between measurement accuracy and speed” (327).
Superposition of Other Sine Waveforms
WavSyn
The WavSyn is a superposition of multiple sine beat waveforms, with one sine beat for each frequency in the SRS spectrum. WavSyn synthesis can be Centered, Aligned Left, Sequential, or Alternating.
-
- Centered alignment builds the sine beat waveforms from the center time of the waveform.
- Aligned Left builds the waveform from the left.
- Sequential builds the waveform from the left with sine beats starting with the highest frequency which optimizes for required peak acceleration.
- Alternating builds the waveform from the left starting with the highest frequency and alternates the polarity of the sine beats which optimizes for required displacement.
The WavSyn waveform was introduced for the simulation of earthquakes. For pyroshock type tests, the WavSyn method produces the necessary short duration, high frequency waveforms.
VibrationVIEW tip: to control the frequency interval of the beats, set the SRS Frequency Resolution parameter to the desired spacing prior to synthesizing the waveform. After synthesizing the waveform, you can set the SRS Frequency Resolution parameter to a different value, and the synthesized waveform will still contain the original spacing.
Damped Sine Waves
Damped sine waveforms are the superposition of multiple sine waves with an exponentially decaying amplitude (damped oscillation). As the amplitude approaches zero, the wave flattens. This waveform can be used to model situations where energy is lost over time.
Conclusion
Various parameters are used to synthesize a pulse equivalent to a specified SRS, including frequency, amplitude, damping ratio, peak time, initial time, and phase. When selecting a waveform, an engineer must consider the waveform shape so the DUT is tested at the correct amplitudes across the frequency domain, the frequency content so the DUT is tested across the same range of frequencies as the real-world waveform, and energy/amplitude so the test has the same amplitude as the real-world waveform.
